-Рубрики
- ЛЮБУЮСЬ! (248)
- НЕ моё (19)
- ♥ МОИ БЛA-БЛA ♥ (1024)
- Жизнизмы (261)
- Фотографии (158)
- Видео (93)
- Даты (89)
- ЛиРу (83)
- Своими руками (74)
- Страна 404 (62)
- Секретики (61)
- Семейное (53)
- Мир, в котором я живу (38)
- Остальное (29)
- ЛиРушечкины встечи (28)
- Политика (26)
- 🚗 Автоистории (21)
- Акции (20)
- Автопробег 2014 (20)
- ☺ Лето 2015 (14)
- Рабочие будни (11)
- Подводки (10)
- Мой голос (7)
- Керчь 2016 🔅 (5)
- Подумалось (5)
- Околорелигиозное (4)
- Масяня (3)
- Здоровье (2)
- Изданное (1)
- МОИ СТИХИ (99)
- Устами младенца (11)
- Видеозал (11)
- Гaлерея (123)
- Живопись и грaфикa (38)
- Фото (83)
- Гермaния (23)
- Aфоризмы (13)
- Музыкa (2)
- Поэзия (5)
- Учебники (2)
- Знания (516)
- Музыкa (12)
- физика (4)
- ЗОЛОТЫЕ РУКИ (2640)
- Бижутерия (60)
- Бутылочки (48)
- Вязaние (40)
- Декупaж (51)
- Кaртинки (229)
- Коробочки-Шкатулочки (88)
- Мастер-классы и схемы (1296)
- Мебель для кукол (35)
- Одеждa для кукол (25)
- Примочки и фишки (245)
- Скрaпбумaгa (104)
- скрапбукинг (239)
- Шaблоны, штaмпы, трaфaреты (128)
- Шьём себе (22)
- Как рисовать (133)
- Winx (5)
- Смешарики (9)
- Новый год (137)
- Отношения (204)
- Оформление дневника (415)
- Кaртинки (55)
- Кнопочки и рaзделители (36)
- Комментaрии (55)
- Ликбез (76)
- МОИ РAМКИ (20)
- Рaмочки (52)
- Смaйлики (18)
- Фоны (27)
- ПЕРЛОВКА (524)
- Aфоризмы (161)
- ЮМОР (224)
- ПИШУТ МОИ ДРУЗЬЯ (182)
- blu Marino (9)
- Валерий Рыбалкин (7)
- Олюнь (4)
- bittern (4)
- annataliya (2)
- Разное (338)
- СТИХоПЛЕТЕНИЕ (269)
- МОИХ ДРУЗЕЙ (51)
- Хозяйке на заметку (113)
- Чудят (29)
-Музыка
- Агата Кристи-Вечная любовь
- Слушали: 383 Комментарии: 0
- I saw you dancing!!!
- Слушали: 6342 Комментарии: 0
- Аргентинское танго)
- Слушали: 1532 Комментарии: 0
- Ванесса Мей
- Слушали: 1975 Комментарии: 0
- Стена
- Слушали: 1162 Комментарии: 0
-Поиск по дневнику
-Статистика
Записей: 6911
Комментариев: 45427
Написано: 77598
Картины,нарисованные с помощью законов математики |
Чтобы создавать подобные психоделические картины вовсе не нужно заниматься духовными практиками, расширяющими сознание. Достаточно просто всерьез заняться наукой. 
Одними из самых известных и красочных картин такого рода являются фрактальные изображения. Сам фрактал при этом представляет собой математическую фигуру, обладающую свойством самоподобия, то есть каждая часть этой фигуры подобна самой этой фигуре. Сегодня существуют специальные программы, позволяющие создавать красивейшие изображения фракталов при помощи компьютера. 
Множество Жюлиа Рассказать, что такое множество Жюлиа, не используя хитроумные специальные математические термины, просто невозможно. Не вдаваясь в математические дебри можно только сказать, что это самоподобная граница множества комплексных чисел, устроенного по определенному закону. Для расчета конкретно этой фотографии использовалась формула (1 − z3 / 6) / (z − z2 / 2)2 + c. 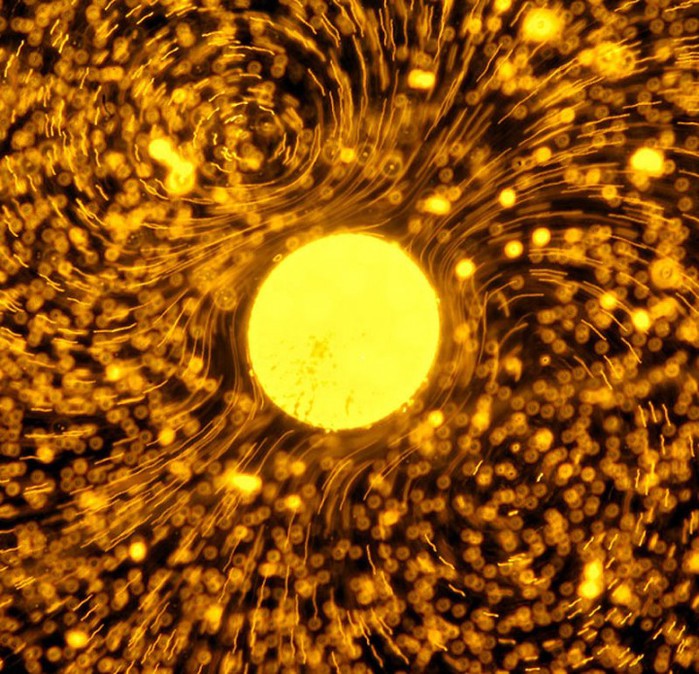
Удивительные водоросли Так выглядит под микроскопом колония одноклеточных водорослей вольвокс. Размер всего шарика, объединяющего от 200 до 50000 клеток, может доходить до 3 мм. Между собой водоросли, члены колонии, скрепляются специальными нитями, внутреннее пространство колонии заполняется слизью, а жгутики водорослей направлены наружу. Вся колония получает возможность двигаться в воде за счет согласованного колебания жгутиков. Вольвоксы живут на Земле уже 200 миллионов лет. 
Мыльный пузырь при 150-кратном увеличении Эта фотография Греда Гюнтера заняла в октябре 18-е место на Конкурсе микрофотографии от Nikon. В тонкой мыльной пленке идет постоянная игра света, поэтому делать такие снимки очень трудно.
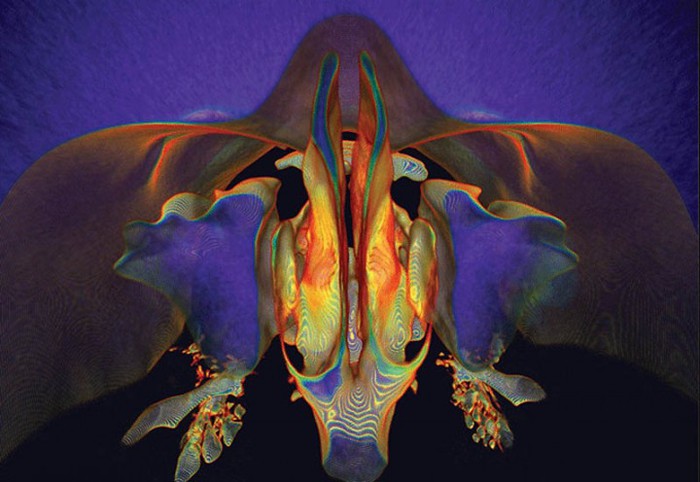
«Что кроется за нашим носом» Этот снимок, сделанный гонгконгским радиологом Кай-хунг Фунг из госпиталя Pamela Youde Nethersole Eastern Hospital, получил главный приз на Международном конкурсе научной и инженерной визуализации (International Science and Engineering Visualization Challenge) в 2007 году. Это изображение было сконструировано путем сведения в один кадр 182-х снимков носа, сделанных при помощи компьютерной томографии. Кости скелета со снимков были удалены, и получилась картинка, представляющая подробное строение носовых пазух. 
Имитация солнечного пятна Этот снимок создан в Национальном центре атмосферных исследований. Для его создания самая полная информация о солнечных пятнах была загружена в сверхмощный компьютер с производительность в 76 терафлопс (76 триллионов операций в секунду). На снимке смоделировано изображение процессов, протекающих на глубине 6000 км от поверхности Солнца. 
Красочный учебник Иллюстрация к главе о человеческой сексуальности из учебника «Биология сегодня» 1972 года. 
Двойное лучепреломление в кристалле кварца Впервые этот эффект был обнаружен в кристаллах исландского шпата. Лучи света, падающие на поверхность кристалла расщепляются на две составляющие. В некоторых случаях это явление дает изумительную по красоте игру цвета. Этот снимок сделан Майком Глейзером из Оксфордского университета. 
Столкновение субатомных частиц Примерно такую картину надеются увидеть ученые, если Большой адронный коллайдер все-таки обнаружит бозон Хиггса, существование которого предсказал в 1960 году шотландский физик Питер Хиггс. Регистрация этого бозона может привести к созданию новой теории мира. 
Пурпурные Гималаи Этот снимок сделан при помощи радиометра ASTER, установленного на борту спутника. Благодаря этому прибору съемку можно вести с разрешением от 15 до 90 м в 14 спектральных диапазонах, начиная от видимого света, заканчивая инфракрасным. Съемка в ближнем инфракрасном диапазоне позволяет создавать очень точные цифровые модели поверхности Земли, а также карты температуры поверхности, ее отражательной способности и т.д. 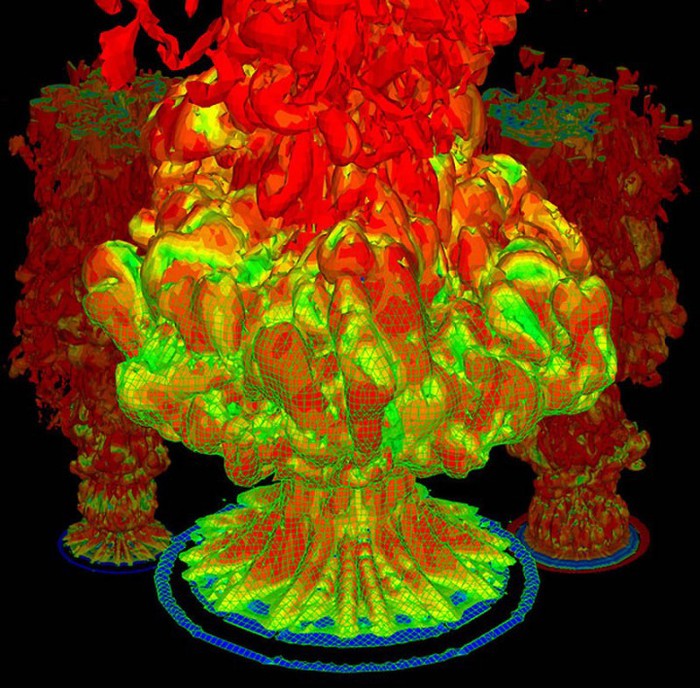
Модель «огненного жара» Эта компьютерная модель пламени была создана в Центре вычислительных исследований университета Баффало Полем Дежареном и его коллегами при проведении ряда экспериментов с огнем. Источник
| Рубрики: | Разное |
Понравилось: 1 пользователю
| Комментировать | « Пред. запись — К дневнику — След. запись » | Страницы: [1] [Новые] |
| Комментировать | « Пред. запись — К дневнику — След. запись » | Страницы: [1] [Новые] |